Este blog está hecho para aquellos a los que les gusta aprender y enseñar matemáticas
sábado, 24 de diciembre de 2011
Cuento de Navidad, con estadística
En una granja, una pavada es alimentada copiosamente durante mil días.
Cada uno de esos días el departamento de estadística de los pavos confirma que la raza humana se preocupa desinteresadamente de su bienestar, con significación estadística cada vez mayor.
El día mil uno (la víspera de Nochebuena) los pavos reciben una sorpresa.
lunes, 19 de diciembre de 2011
¡¡Feliz Navidad!!
El Departamento de matemáticas, con este navideño triángulo de Tartaglia, desea a todos los seguidosres de Aprender y enseñar Matemáticas la paz y la auténtica alegría a la que nos invita la Navidad.
Especialemente en estas fechas, deseamos compartir con todos vosotros la esperanza en un mundo más justo, solidario y fraternal.
domingo, 18 de diciembre de 2011
Un texto de geometría, de Suárez Somonte, sin fórmulas ni figuras. La didáctica por encima de los contenidos. Alegato contra el memorismo.
Don Ignacio Suárez Somonte (1865-1951) fue catedrático de Matemáticas, en el Instituto del Cardenal Cisneros. Hombre preocupado por la enseñanza y su metodología, fue director del Instituto de 1918 a 1931. Durante la dictadura del general Primo de Rivera desempeñó la Dirección General de Primera Enseñanza. Se jubiló en 1935. Escribió varios libros de texto de Matemáticas para las enseñanzas medias.
[Necrlógica en el ABC de 12/10/1951]
Esta es la referencia biográfica de Ignacio Suárez Somonte que figura en memoria del Instituto Cardenal Cisneros que se editó en 1945 con motivo del centenario de la fundación del Instituto. La versión digitalizada de esta memoria se puede consultar aquí.
Una referencia fundamental para conocer los promenores de la actividad de Ignacio Suárez Somente en el Instituto del Cardenal Cisneros es el libro de las profesoras Gloria González y Begoña Talavera, "El Instituto del Cardenal Cisneros. Crónica de la enseñanza secundaria en España (1845-1975). Páginas 130, 131 y 132.
Estos son algunos de losl ibros de texto de Suarz Somonte
Para completar esta reseña de la vida y las ideas pedagógicas de Ignacio Suárez Somonte, copiamos una parte del texto de una conferencias en la que él expone su propio caso como ejemplo de cómo los exámenes de ingreso en las Esculeas Especiales cerraban el paso a los pobres.
El título de la conferencia en al academia de Jusrisprudencia en 1920 se titula "De la escuela a la Universidad".
CONFERENCIA AUTOBIOGRÁFICA
Vosotros conoceréis muchos casos de vocaciones cortadas, de aptitudes paralizadas por ese dique de no poder pagar la preparación de una carrera especial. Yo no resisto la tentación de contaros un caso, que me toca muy de cerca. Un niño de familia pobre y humilde; en el pueblo, un colegio subvencionado por el Ayuntamiento, lo que da lugar a una beca que se obtiene por oposición; el niño entra así. La beca no significa más que el pago de los estudios; los libros son los de sus compañeros; las matrículas, como se obtienen por oposición, es cuestión del primer año, y en ese período de su segunda enseñanza, al mismo tiempo que despacha drogas en una farmacia, se define su afición, le gustan las matemáticas, le agradan las construcciones, y el adolescente se cree un ingeniero en ciernes, más se entera de ese camino que hay que recorrer; imposible. Firme en su vocación y en su fuerza de voluntad, espera enseñando matemáticas en su pueblo en una Academia de Telégrafos; llega la fecha de los diez y nueve años, en que las clases pobres pagaban entonces el honroso tributo de su sangre, de servir a su Patria y a su Rey, y siendo soldado, hace los tres primeros años de Facultad con programas de la Escuela de Ingenieros a la vista, para ajustar a ellos su cultura, porque él decía, si no valen asignaturas aprobadas, valdrán conocimientos adquiridos, y, firme en su voluntad, entonces aparece otro escollo más; la creación de la escuela politécnica: más gastos, más entretenimiento, más pérdida de tiempo, no puede ser y sigue estudiando la carrera de Ciencias (que esa como carrera libre, la pueden seguir los pobres) y llegar a ser Catedrático y Director de Instituto y a tener el honor de dirigiros la palabra.
“De la escuela a los estudios superiores”. Conferencia en la Real Academia de Jurisprudencia y Legislación de D. Ignacio Suárez Somonte. 1920.
En este enlace se pueden contemplar algunos detalles de la vida de Ignacio Suárez Somonte http://felixpineroradiointerior.blogspot.com/2019/08/ignacio-suarez-somonte-director-general.html?m=1
El libro de Nociones de Geometría de Ignacio Suárez Somonte no deja de ser original, por no decir: extravagante.
Este texto estaba destinado a los alumnos de bachillerato (12 o 13 años). Llama poderosamente la atención que el libro no tenga ni fórmulas ni figuras. En él todas las construcciones y demostraciones se enuncian de una manera descriptiva. El autor, dando las pertinentes indicaciones, deja para el alumno la construcción de las figuras o la deducción de las fórmulas por si mismo.
En los años 30 mi padre fue alumno del Instituto del Cardenal Cisneros, en donde era catedrático Suarez Somonte. Este libro de Nociones de Geometría de D. Ignacio Suarez Somente, lo conocí de niño, pues era el libro en el que había estudiado mi padre (un gran amante de la geometría). Así pues, este libro siempre lo he tenido muy a mano en casa, pero a nadie sensato se le ocurriría utilizarlo como libro de consulta, como pasa con otros textos.
Aunque esto es un comentario marginal, que quizá no proceda aqui, a mi juicio, en España los libros de texto de Matemáticas anteriores a estas fechas eran muy deficientes en sus contenidos y en su concepción. Eran confusos, con contenidos mal escogidos, y no tenían ni aplicaciones prácticas, ni ejercicios, ni planteamientos didácticos. La comparación de loos textos españoles con otros textos coetaneos provenientes de Francia, Inglaterra y Estados Unidos, como los Bruño, FTD, FGM etc. no resiusten comparación.Por eso a mi entender fueron muy inmnovadores los libros de texto de bachillerato que en los años treinta hicieron Rey Pastor y Puig Adam.
La didáctica tan singular de Ignacio Suarez Somonte hace necesaria una explicación. La justificación viene expresada en un prólogo vehemente, que es un alegato contra el memorismo.
El memorismo es una constante del sistema de enseñanza secundaria basada primordialmente en exámenes y reválidas y en el que los profesores no toman iniciativas de innovación.
Para entender el contexto de la época hay que tener en cuenta que por aquel entonces la mayoría de los alumnos del bachillerato acudía al Instituto sólo a examinarse y que tradicionalmente la formación científica y matemática en España de los profesores de ensñanza media era apenas existente. No había suficientes profesores cualificados para enseñar el método científico y la lógica matemática. En aquella época los exámenes de Matemáticas eran orales y consistían en que los alumnos delante de una pizarra y ante un tribunal tenían que exponer un tema del "Programa". El tema lo elegía el Tribunal. La nota dependía de la brillantez de la exposición y de la precisión en la resolución de las preguntas que le planteaba el tribunal sobre alguna cuestión o problema. De este método de examen tengo constancia directa de mi padre, que fue uno de los niños que acuadia al Instituto del Cardenal Cisneros a examinarse.
Lo que es manifiesto es que Suarez Somente sacrificó los contenidos a la didáctica. El método de razonar pasó a ser el objetivo fundamental de la clase de Geometría.
Además de la cuestión formal, a la que nos hemos referido, del libro de Suárez Somonte llama la atención la distribución de los contenidos. Por un lado aparecen los conceptos geométricos (segmentos, ángulos, figuras, áreas y volúmenes) y sus relaciones, pero se pasan por encima todo lo que suponen cálculos y problemas prácticos de aplicación.
Veamos una muestra del libro. En la que se demuestra el Teorema de Pitágoras a partir de las relaciones de semejanza:
Por lo que se ve Ignacio Suarez Somonte era un hombre con personalidad y el hecho de ir contra el sistema (con razón) le llevaba a radicalizar posturas e imponer con la fuerza de su libro de texto sus puntos de vista. No cabe duda que a comienzos del siglo XX, ser catedrático del "Cisneros" daba mucha influencia.
Como testimonio para la historia, he escaneado el Prólogo y lo he convertido en texto utilizando un programa de OCR on-line, que funciona fenomenal: http://www.onlineocr.net/
Para los curiosos, copio íntegro el Prólogo de
Nociones de Geometría
Por Ignacio Suárez Somonte
Catedrático de Matemáticas
en el Instituto del Cardenal Cisneros de Madrid
1914
(El subrayado es mío)
PRÓLOGO
No soy de los que opinan que la memoria es privilegio de los tontos, pero sí de los que creen que cultivar la memoria con la predilección que se hace entre nosotros es un grave error, un mal fecundo, cuyos efectos son el atraso y las debilidades de nuestro pueblo y cuyas causas forman numerosos ciclos en los cuales entramos todos.
Yo he visto con honda pena niños que en la escuela recitaban con alegre sonsonete las reglas de la división sin saber multiplicar, y alumnos que en los exámenes de Matemáticas repetían con todas sus letras, con sus puntos y sus comas, las lecciones que les había tocado en suerte, sin omitir nada de sus rigurosas demostraciones, sin perder un detalle de sus rígidas figuras, y todo esto sin moverse de la silla, sin salir al encerado, sin entender lo que decían.
Esto, que yo he visto muchas veces y que han observado todos los que se dedican á la enseñanza, no es ya, simplemente un error, es un delito á que debiera asignarse castigo en el Código penal.
Los culpables de ese delito no son el niño ni el alumno: ellos son las víctimas de tal atentado á la razón. El profesor, si es que tal nombre merece quien así pretende enseñar, es el culpable en algunos casos, y en otros lo son las absurdas é imposibles circunstancias y condiciones en que se da esa clase de enseñanza que así viciada debiera llamarse infanticidio intelectual.
Cuanto se haga para evitarla será obra de libertad y de bien común.
La cátedra, el examen y el libro caen dentro de la esfera de acción del catedrático: y desde ellos se puede, se debe combatir y poner trabas á ese enemigo de la razón llamado memorismo, que esclaviza la inteligencia, seca las fuentes del entendimiento y extenúa las fuerzas de la voluntad, creando así espíritus débiles para la lucha de la vida é inútiles para la obra del progreso.
En esta Geometría el alumno no puede aprender de memoria ni las demostraciones ni las figuras á que aquéllas se refieren, porque ni hay figuras en el libro, ni en rigor hay en él demostraciones.
Los párrafos que siguen á los enunciados de los teoremas ó de los problemas indican el camino que hay que seguir para demostrar los primeros ó para resolver los segundos. El que siga ese camino demostrará los teoremas y resolverá los problemas razonando por su propia cuenta sobre figuras dibujadas por él y hechas sin traba alguna de posición impuesta, que conduce muchas veces á error en los libros de Geometría con figuras.
¿Que hay profesores que buscan las figuras en otros libros y se las entregan á sus alumnos, á los que ordenan ó consienten que aprendan de memoria esos párrafos? Por desgracia sí los hay. Y bien podían esos señores dejar la enseñanza de estas materias y dedicarse á otra cosa que sea más de su competencia, y los padres de esos alumnos bien pueden fijarse en que ese lastre inútil con que se carga la memoria de sus hijos son los primeros pasos que éstos dan en el camino que conduce á la peor de las esclavitudes, á la esclavitud de la inteligencia.
Á los alumnos que estudien este libro les diré que por nada ni por nadie aprendan de memoria esos párrafos á que me vengo refiriendo; porque la memoria en estas materias sólo debe cargarse con lo que vea claro la razón. Para estudiar esta Geometría debe tenerse el libro abierto á la izquierda, enfrente una hoja de papel y en la mano un lápiz; ir trazando en el papel lo que en esos párrafos se vaya ordenando y, fija la atención en el razonamiento que se vierte sobre la figura que se va trazando, se llega al fin con la figura dibujada y la demostración hecha ó el problema resuelto. Después, apartando la vista del libro, se repite una y otra vez el razonamiento, construyendo siempre nuevas figuras y no cuidando de que éstas tengan siempre la misma posición ni sus elementos igual tamaño, antes bien, conviene que varíen en lo uno y en lo otro. El alumno debe hacer estas repeticiones en voz alta, poniendo especial cuidado en hablar en primera persona ó en gerundio, porque él es el que traza la figura, el que razona y discurre, el que recuerda verdades necesarias para el razonamiento; él es quien demuestra: no es el profesor, ni el autor, ni el libro.
Para que en esas repeticiones en voz alta se exprese el alumno con lenguaje propio y forma adecuada á los actos que realiza ó á los razonamientos que hace, conviene tenga presente los siguientes cambios ó sustituciones:
La frase —Para demostrar esto— con que suelen empezar esos párrafos que siguen á los enunciados de los teoremas, debe el alumno sustituirla por esta otra —En efecto.
En cada frase de mandato ó consejo para trazar la figura debe el alumno colocar el verbo en primera persona del presente de indicativo, ó mejor aún en gerundio, dando á continuación nombre al elemento de la figura que traza cuando ejecuta ese mandato.
Y tanto al estudiar con el libro abierto como al hacer -esas repeticiones en voz alta, cuando el libro expresa ó manda que se formen relaciones entre los elementos de la figura construida, debe el alumno escribir esas relaciones, representando en ellas cada elemento por las letras que tenga en la figura.
Á los profesores que enseñen por este libro, lisa y llanamente les diré el método de enseñanza que yo llevo en mi clase.
En los primeros meses de curso mi clase es, en rigor, sala de estudio.
Un alumno lee en voz alta esos párrafos, en los que se indica el camino que hay que seguir para demostrar los teoremas ó resolver los problemas.
Uno ó más alumnos los traducen en el encerado, en el cual van apareciendo los elementos de la figura á medida que el razonamiento leído lo exige. Los demás alumnos, con el libro abierto, ó sin él, ven y escuchan. cómo de esos párrafos brotan de un modo claro las figuras geométricas y cómo los razonamientos hechos se ajustan á ellas, aunque están trazadas con absoluta libertad.
Yo, entretanto, me coloco en segundo lugar: soy ayudante de los alumnos, ya deteniendo al que lee para aclarar ó fijar algún concepto, ya para guiar á, los que se hallan en el encerado, ya para hacer ver con repeticiones útiles la equivalencia entre lo que uno lee y lo que dibujaron los otros.
Después de todo esto, el alumno aún no sabe la demostración; sabe cómo se demuestra si la escena anterior se repite lo suficiente. Pero esto no es bastante: hay necesidad de repetir una y otra vez las demostraciones -con el libro cerrado. De él tomamos antes lo necesario para la demostración. Ahora hay que hacerla, y éste es el momento crítico, aquí está la misión más delicada y más alta del profesor.
El alumno tenderá á repetir muchas palabras del libro, que no deben ser dichas por él, porque el libro no ejecuta: manda ó aconseja, y esas palabras de mandato ó consejo no deben ser pronunciadas por el alumno. El profesor debe hacer que el alumno las sustituya por otras equivalentes y apropiadas a la acción que el mismo ejecuta; y de este modo, con este trabajo constante y repitiendo cuanto sea necesario con un mismo alumno ó con alumnos distintos, se llega á conseguir (yo os lo aseguro) que una gran mayoría de ellos demuestre los teoremas y resuelva los problemas, discerniendo por cuenta propia, expresándose con sus propias palabras y hablando cada uno su propio y natural lenguaje.
Entonces ya puede el profesor estar satisfecho, porque sólo entonces ha cumplido su misión y su deber. Y también el alumno está contento y llega á creerse, con sobrada razón, que aquellos conceptos ó aquellas verdades que se le enseriaron son ya suyos y le pertenecen, porque han dormido en su espíritu y los expresa con el ropaje de su propio estilo.
El que por vez primera siga ese método en la enseñanza de la Geometría llegará, á desconfiar del éxito y sentirá temores al ver lo poco que avanza en la asignatura. Que no le importe: yo también tuve esas dudas y sentí esos temores el primer ano, al ver pasados casi cuatro meses del curso, bien menguado ya por las largas vacaciones de Navidad, cuando mis alumnos habían aprendido á demostrar, en la forma antes dicha, y no llevábamos dada ni la cuarta parte de la asignatura; es decir, que por aquella época mis alumnos sabían razonar, pero sabían muy poca Geometría (Yo, amante de esta Ciencia, declaro que vale mucho más saber razonar que saber Geometría). Bien pronto se desvanecieron mis temores por el atraso de la, clase al convencerme de que ésta estaba ya en condiciones de seguir el camino de la asignatura con la velocidad que fuera preciso.
Desde entonces la clase varía de aspecto, el alumno sabe ya estudiar y se le puede exigir que estudie sin explicarle previamente más que aquellos puntos que puedan presentar serias dificultades. De este modo, no encontrando el alumno al estudiar obstáculos que no pueda vencer, estudia con gusto y corre en la asignatura, de tal suerte que saca con holgura el atraso de los primeros meses.
El profesor que siga este método, someta á sus alumnos en el mes de Mayo á ejercicios escritos sobre un punto cualquiera de la asignatura, y verá cómo esos ejercicios escritos por diferentes alumnos que han estudiado por el mismo texto y con el mismo profesor no se parecen más que en el fondo; en la forma son distintos: varían en las palabras, en el estilo, en las posiciones de las figuras y en el tamaño de sus elementos.
¿Qué mayor prueba de que los alumnos que tal hacen se han posesionado de esas verdades geométricas, y lo que es aún más importante, saben estudiar y discurrir por cuenta propia?
Con la inmensa mayoría de los libros elementales de Geometría y de los profesores que á esta enseñanza se dedican se pueden formar dos grandes grupos.
Unos que colocan ó enseñan en los preliminares de la Geometría unas nociones de triángulos y de igualdad de los mismos, con el propósito de servirse de ellas en las demostraciones de una multitud de teoremas que forzosamente han de preceder a la teoría general de polígonos.
Y otros, que no hacen tal dislocación, demuestran esos teoremas sin servirse de los triángulos.
Este libro, sólo para las demostraciones correspondientes a los párrafos 78 y 79 y primera parte del 86 es conveniente en algunos casos el auxilio de la igualdad de triángulos; y en mi clase, cuando estos casos llegan, de la igualdad de triángulos hago uso; creo, por tanto, que cada profesor puede y debe hacer lo mismo, tanto en este caso como en todos aquellos en que la demostración del libro pueda sustituirse por otra que sea más sencilla o pueda ser más fácilmente aprendida por el alumno.
Sólo así, con tal libertad, puede tener la misión de enseñar su propia y natural dignificación, y ser el libro de texto lo que debe ser y es en rigor: guía seguro del que estudia y orientación amplia del que enseña.
Foto del acto de homenaje a D. Ignacio Suarez Somonte con motivo de su jubilación en 1935. Esta foto procede de la exposición que se realizó con motivo del 150 aniversario de la creación del Instituto del Cardenal Cisneros
APLICACIÓN DIDÁCTICA
Recrear con los alumnos una clase de Ignacio Suárez Somonte.
En el curso 2013_14 recreamos con alumnos de 4º de la ESO una clase de Suárez Somonte. Concretamente la lección del teorema del seno . Fue un éxito completo. Los alumnos salieron encantados y se aprendieron la demostración estupendamente. Luego la aplicaban con soltura para hacer problemas. Espero detallar en otra entrada con más detalle, todo lo relacionado con esta actividad.
martes, 13 de diciembre de 2011
Máquinas de lógica binaria
"Oigo y olvido,
veo y recuerdo,
hago y entiendo."Seguimos buscando y rebuscado ideas para hacer un Gabinete de Matemáticas. Un proyecto no es el final, es el principio de nuevas ideas que nos llevan cad vez más lejos. Las Matemáticas están detrás de la tecnología. En el Canal UNED hemos encontrado estos vídeos.
Nos identificamos con la filosofía pedagógica que se hace en la presentación que abre cada vídeo.
"Para trabajar con la lógica binaria no es preciso recurrir siempre a la microinformática ... Los objetos caseros se pueden prestar al trabajo matemático y provocar fórmulas de pensamiento abstracto a niveles de profundidad interesantes dentro de uncontexto, ¿por qué no declararlo como lo que es?, lúdico.
Todo lo que sigue es algo así como la víua del tren, pero con algunos tramos intencionadamente sin construir. Todo lo que sigue puede parecerse a la narración de una historia, de un cuento, con su "colorín colorado"; pero no es cierto. Cuando te parezca que se ha llegado al final, en ese momento te estará esperando el lobo que te raptará y tem llevará, quieras o no, a lugares diferentes, y te encontrarás tratando de resolverotros problemas distintos de los que aquí se han propuesto, o queriendo construir el puente que faltaba en esa vía del tren, intentando resolver cualquiera de los retos intermedios que han quedado tan solo apuntados."
Máquinas de lógica binaria. Las mil y una bolas
http://www.canaluned.com/carreras/psicopedagogia/maquinas-con-logica-binaria-i---las-1001-bolas-1580.html
Máquinass de lógica binaria. El gato con botes
http://www.canaluned.com/carreras/psicopedagogia/maquinas-con-logica-binaria-ii---el-gato-con-botes-1547.html
http://www.canaluned.com/carreras/psicopedagogia/maquinas-con-logica-binaria-iii---el-xilofonista-de-hamelin-1581.html
Ciencia en acción. Aprender ciencia con los sentidos
"Oigo y olvido,
veo y recuerdo,
hago y entiendo."
Ciencia en acción es un certamen anual en el que se presentan propuestas para enseñar las Ciencias a través de experimentos y todo tipo de artefactos. También hay muchos ejemplos de actividades matemáticas. He aqui un ejemplo, pero hay muchos más.
Ciencia en acción I
Programas de CIENCIA EN ACCIÓN en el Canal UNED:
- Ciencia en acción II
- Ciencia en acción III
- Ciencia en acción IV
- Ciencia en acción V
- Ciencia en acción VI
- Ciencia en acción VII
- Ciencia en acción VIII
- Ciencia en acción IX
- Ciencia en acción X
- Ciencia en acción XI
- Ciecia en acción XII
- Ciencia en acción XIII
- Ciencia en acción IV
- Ciencia en acción XV
- Ciencia en acción XVI
- Ciencia en acciópn XVII
- Ciencia en acción XVIII
- Ciencia en acción XIX
- Ciencia en acción XX
- Cinecia en acción XXI
- Cinecia en acción XXII
- Ciencia en acción XXIII
- CIencia e acción XXIV
- Ciencia en acción XXV
- Ciencia en acción XXVI
- Ciencia en acción XVII
- Ciencia en acción XXVIII
- Ciencia en acción XXIX
- Ciencia en acción XXX
- Ciencia eb acción XXXI
- Ciencia en acción XXXII
- Ciencia en acción XXXIII
- Ciencia en acción XXXIV
- Ciencia en acción XXXV
Arquímedes, el genio de Siracusa
En Canal UNED hemos encontrado este vídeo sobre Arquímedes.
Ningún sabio como Arquímedes supo relacionar la intuición de los arttilugios mecánicos con las más profundas ideas matemáticas.
Seguimos indagando propuestas para nuestro Gabinete de Matemáticas.
Ningún sabio como Arquímedes supo relacionar la intuición de los arttilugios mecánicos con las más profundas ideas matemáticas.
Seguimos indagando propuestas para nuestro Gabinete de Matemáticas.
martes, 6 de diciembre de 2011
Dibujar gráficas de funciones usando el buscador de GOOGLE
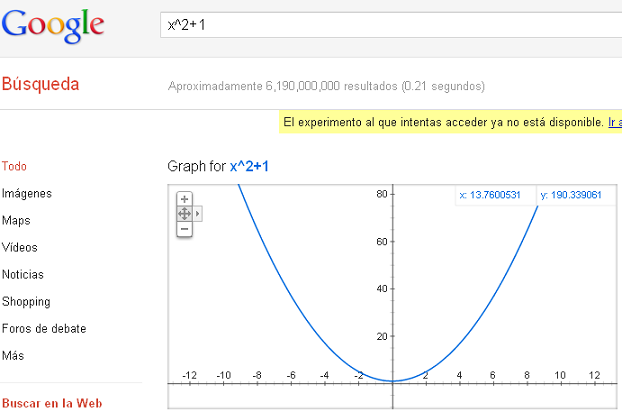
Siguiendo a Gaussianos nos hemos enterado de la nueva posibilidad del buscador de GOOGLE. Ahora se pueden dibujar gráficas de funciones, simplemente escribiéndolasa en el buscador. ¡¡Increíble!!
Copiamos aquí la entrada:
Me entero a través de una mención de bolorsociedad en Twitter (que también hicieron después javierarmentia y DrCooper3_14) que a partir de ayer mismo ya se pueden representar gráficamente funciones (por ahora únicamente de una variable) con Google. Sí, sí, con el buscador. Simplemente hay que escribir en la caja de texto habitual la expresión de la función que queramos representar y nos aparecerá la gráfica de la misma como primer resultado de la búsqueda. Y en este punto no está de más recordar que las potencias se escriben con el símbolo ^ (por ejemplo x^3 representa a) y las raíces cuadradas con sqrt (por ejemplo, sqrt(x) representa a
).
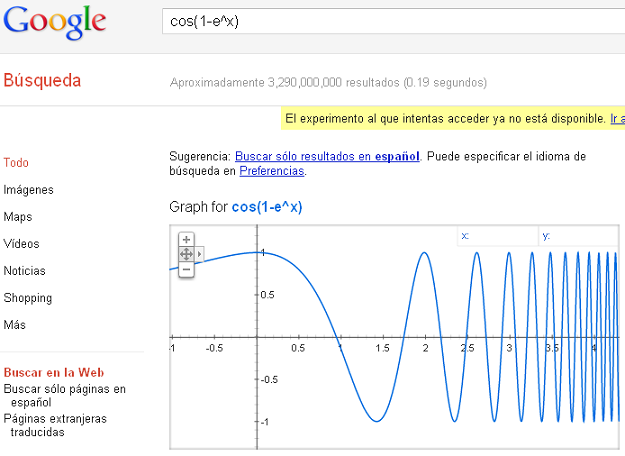
Como ejemplo de representación, ésta es la de:
Según este post del blog oficial de Google, esta nueva función nos da la posibilidad de representar gráficamente una gran cantidad de funciones, incluyendo trigonométricas, exponenciales, logarítmicas, y composiciones de todas ellas.
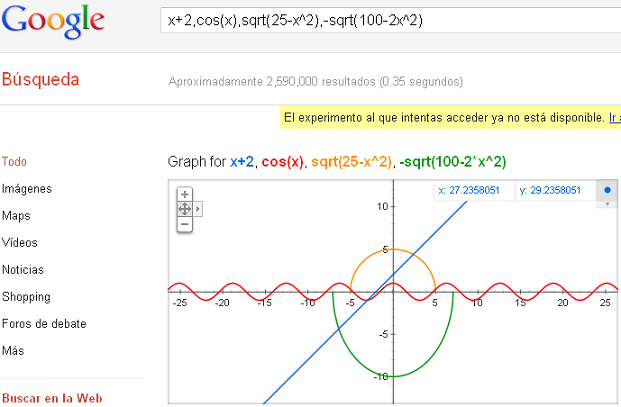
Por otra parte, también se puede representar varias funciones a la vez. Por ejemplo, así queda la representación conjunta de:
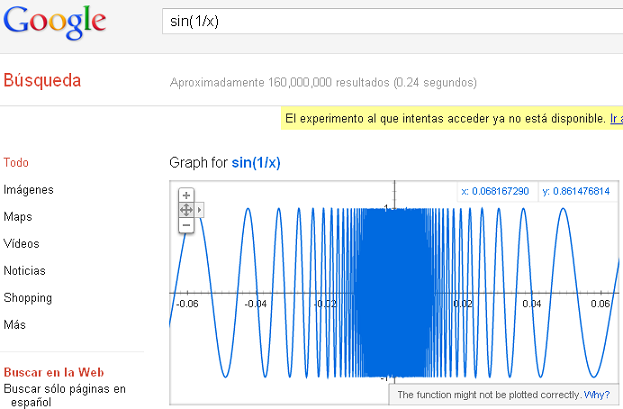
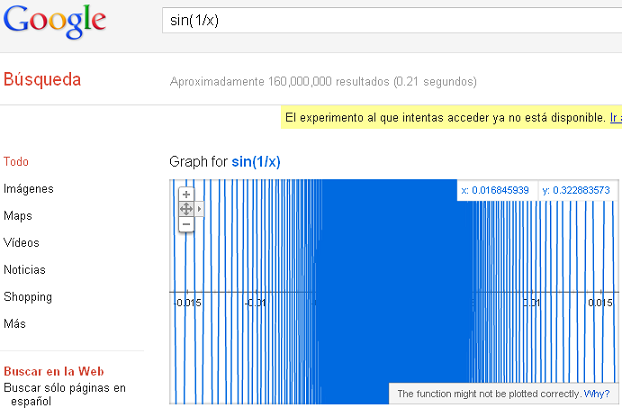
También se puede hacer zoom en las gráficas. Vamos a hacerlo con la función:
Vamos, que a partir de ahora con Google podemos dibujar desde la función
Zoom de acercamiento
Zoom de alejamiento , por cuya gráfica me han preguntado por mail hace poco
como este corazón que nos enseñan a dibujar en el blog de Google. Una nueva opción de Google que aunque está comenzando parece que promete.
domingo, 4 de diciembre de 2011
Las matemáticas no dan más que problemas. Unos problemillas para pensar en el puente

1. LOS NÚMEROS PRIMOS SON INFINITOS, PERO ...
Alumno: entonces, ¿los primos son infinitos?
Maestro: Así es, ya lo demostró Euclides hace muchísimos años.
Alumno: Entonces, ¿es imposible saber cuántos primos hay terminados en 1, cuántos terminados en 3, cuántos terminados en 7 y cuántos terminados en 9?
Maestro: Así es, pero sin embargo, te puedo decir cuál es último dígito del producto de todos los primos que existen...
Alumno: ?
2. LA CUADRATURA DEL CÍRCULO
Un problema que trajo de cabeza a los griegos fue el de la Cuadratura del circulo. El problema consistia en dado circulo, construir, utilizando sólo la regla y el compás, un cuadrado de su misma área.
Pasados dos mil años, en el el siglo XVIII, se demostró que es imposible hacerlo.
Viendo el dibujo siguente, en el que un circulo, de radio R, rueda sobre su circunferencia, calcula el área del cuadrado. [Puedes utilizar que la longitud de una circunferencia es longitud = 2 * pi * radio

[Fuente: "Proofs without words". Roger. B Nelsen]
Polígonos regulares. Un proyecto para hacer usando listones de madera
Seguimos con nuestra idea de aprender haciendo, trabajar con proyectos y construir un Gabinete de matemáticas.
Este es el proyecto que ahora nos proponemos:
Costruir, utilizando listones de madrea, una colección de polígonos regulares (su perímetro).
Queremos que:
a) Todos los polígonos (triángulo equilátero, cuadrado, pentágono rehular, hexágono regular, heptágoino regular y octógono regualr) tengan las dimensiones adecuadas para que se inscriban en la misma circunferencia.
 b) El tamaño sea adecuado para que se puedan utilizar con fines didácticos en una clase.
b) El tamaño sea adecuado para que se puedan utilizar con fines didácticos en una clase.Tienen que servir como plantilla para dibujar en la pizarra.
También tienen que poderse utilizar para que sobre ellos se puedan señalar los elemntos de un polígono (lados, perímetro, vértices, angulos, diagonales, apotema, ejes de simetría, radios inscrito y circunscrito, .....). Para señalar estos elementos se pueden utilizar cordeles de colores, alambres, regletas, etc.
c) El material básico tiene que ser listones de madera encolada y la estructura debe ser lo suficientemente resistente como para que se pueda manejar sin problemas y se le piedan añadir cuerdas, clavitos, asas, ..... Tiene que ser algo parecido a las escuadras y los cartabones para pizarra.
Problemas que nos surgen
1. Hay que calcular las dimensiones de los lados de cada uno de los polígonos regulares en función del radio de la circunferencia circnscrita. Para esto se puede usar trigonometría, o Geogebra.
2. Hay que hacer planos, cropquizar y hacer un despiece acotado.
3. Hay que determinar el ángulo de los ingletes que enlazan los lados en cada uno de los polígonos. Hay que hacerse una caja ingletadora.
4. Hay que resolver los problemas constructivos para dar rigidez a la estructura. Además del encolado se pueden usar grapas o unos perfiles metálicos qe se usan en el enmarcado.
Y ahora... manos a la obra,... nos ponemos a darle vueltas a la cabeza, a buscar información, a conseguir herramientas, a hacer croquis, a ampliar los objetivos y mejorar lo que ya tenemos ....
jueves, 1 de diciembre de 2011
Nicanor Parra, un matemático, premio Cervantes 2011
Hoy se ha hecho pública la concesión del premio Cervantes 2011, al poeta izquierdista chileno de 97 años, Nicanor Parra.
Nicanor Parra es el hermano mayor de la cantante fallecida Violeta Parra. Su profesión fue la de profesor e investigador en Física Matemática.
Biografía de Niocanor Parra
Es muy interesante este AUTORRETRATO de Nicanor Parra, en el que hace referencia a su duro trabajo como profesor de Matemáticas.
Esto es un prueba más de que las Matemáticas no son incompatibles con la poesía y la literatura. Por ejemplo, El premio Nobel de literatura, el español José Echegaray, era matemático. Bertrand Russell, también premio Nobel de Literatura, era Matemático. También científico era Ernesto Sábato.
Nicanor Parra es el hermano mayor de la cantante fallecida Violeta Parra. Su profesión fue la de profesor e investigador en Física Matemática.
Biografía de Niocanor Parra
Es muy interesante este AUTORRETRATO de Nicanor Parra, en el que hace referencia a su duro trabajo como profesor de Matemáticas.
Autorretrato
Considerad, muchachos,
Este gabán de fraile mendicante:
Soy profesor en un liceo obscuro,
He perdido la voz haciendo clases.
(Después de todo o nada
Hago cuarenta horas semanales).
¿Qué les dice mi cara abofeteada?
¡Verdad que inspira lástima mirarme!
Y qué les sugieren estos zapatos de cura
Que envejecieron sin arte ni parte.
En materia de ojos, a tres metros
No reconozco ni a mi propia madre.
¿Qué me sucede? -¡Nada!
Me los he arruinado haciendo clases:
La mala luz, el sol,
La venenosa luna miserable.
Y todo ¡para qué!
Para ganar un pan imperdonable
Duro como la cara del burgués
Y con olor y con sabor a sangre.
¡Para qué hemos nacido como hombres
Si nos dan una muerte de animales!
Por el exceso de trabajo, a veces
Veo formas extrañas en el aire,
Oigo carreras locas,
Risas, conversaciones criminales.
Observad estas manos
Y estas mejillas blancas de cadáver,
Estos escasos pelos que me quedan.
¡Estas negras arrugas infernales!
Sin embargo yo fui tal como ustedes,
Joven, lleno de bellos ideales,
Soñé fundiendo el cobre
Y limando las caras del diamante:
Aquí me tienen hoy
Detrás de este mesón inconfortable
Embrutecido por el sonsonete
De las quinientas horas semanales.
Antipoemas, de Nicanor Parra
Esto es un prueba más de que las Matemáticas no son incompatibles con la poesía y la literatura. Por ejemplo, El premio Nobel de literatura, el español José Echegaray, era matemático. Bertrand Russell, también premio Nobel de Literatura, era Matemático. También científico era Ernesto Sábato.
Manifiesto de Nicanor Parra
Volver a los 17 (Violeta Parra)
miércoles, 23 de noviembre de 2011
"Mathematical Education in Europe". Un interesante informe de EURYDICE
Presentación:
La competencia en las matemáticas es esencial para una amplia gama de disciplinas, profesiones y áreas de vida. Este informe Eurydice revela elementos cruciales de las políticas y prácticas que dan forma a la ennseñanza de matemáticas en los sistemas educativos europeos, centrándose en las reformas de las matemáticas planes de estudio, enseñanza y métodos de evaluación, así como la formación del profesorado.
El informe también explora cómo hacer frente a los países de bajo rendimiento y aumentar la motivación de los alumnos para aprender las matemáticas. Se basa en una extensa revisión bibliográfica sobre la enseñanza de las matemáticas, la principal los resultados de los estudios internacionales PISA y TIMSS, e incluye los resultados de una la encuesta piloto de Eurydice (SITEP) sobre el contenido de los programas iniciales de formación del profesorado. cubre 31 países (todos los Estados miembros de la UE, más Islandia, Liechtenstein, Noruega y Turquía) y se el año de referencia 2010/11.
Contenidos
Prólogo
Introducción
Resumen
El rendimiento en matemáticas: datos de las encuestas internacionales
Grandes encuestas sobre las matemáticas: TIMSS y PISA
El logro en Matemáticas de acuerdo a los resultados de PISA
El logro en Matemáticas el logro de acuerdo a los resultados de TIMSS
Principales factores asociados con el rendimiento en matemáticas
Capítulo 1: El currículo de matemáticas
Introducción
1.1. Elaboración, aprobación y difusión de los documentos de matemáticas de dirección
1.2. La revisión del currículo de matemáticas y el seguimiento de su eficacia
1.3. Objetivos de aprendizaje y contenido de las matemáticas y las competencias en el currículo
1.4. Tiempo enseña dedicada a la enseñanza de las matemáticas
1.5. Los libros de texto y material didáctico en matemáticas
Resumen
Capítulo 2: Enfoques de enseñanza, métodos y organización en el aula
Introducción
2.1. Gama de métodos de enseñanza: directrices y prácticas
2.2. Organización del aula: la agrupación de alumnos de
2.3. Uso de las TIC y las calculadoras en el aula de matemáticas
2.4. Asignación de tareas 64
2.5. Las encuestas nacionales y los informes para apoyar la política basada en la evidencia sobre la enseñanza de las matemáticas métodos
Resumen
Capítulo 3: Evaluación de las Matemáticas
Introducción
3.1. Mejorar el aprendizaje a través de formas diversas e innovadoras de evaluación de
3.2. El papel de las pruebas nacionales
3.3. Matemáticas en la educación secundaria superior
3.4. Uso de las matemáticas de evaluación de datos
3.5. Las encuestas nacionales y los informes de las políticas basadas en la evidencia sobre la evaluación de
Resumen
Capítulo 4: Abordar el logro de baja en Matemáticas
Introducción
4.1. Políticas basadas en pruebas sobre el bajo rendimiento
4.2. Las principales conclusiones de investigación sobre medidas eficaces para abordar el bajo rendimiento
4.3. Políticas nacionales para mejorar los logros de
4.4. Tipos de apoyo para alumnos con bajo rendimiento
Resumen
Capítulo 5: Mejorar la motivación del estudiante
Introducción
5.1. Proporcionar un marco teórico y basada en la evidencia
5.2. Estrategias nacionales para mejorar la motivación del estudiante en el aprendizaje de las matemáticas
5.3. Actividades de apoyo central para mejorar las actitudes hacia el aprendizaje de las matemáticas
5.4. Cuestiones de política relacionadas con la escasez de habilidades y la asimilación de las matemáticas en la educación superior
Resumen
Capítulo 6: Educación y Desarrollo Profesional de Maestros de Matemáticas
Introducción
6.1. Los retos demográficos de la profesión docente de matemáticas en Europa
6.2. Lograr el equilibrio adecuado en el contenido de la formación inicial
6.3. La importancia de la continua basada en el sujeto, el desarrollo profesional de colaboración
6.4. La educación inicial para las matemáticas / los profesores de ciencias: generalista y programas especializados
Sitep 130 resultados
Resumen 140
Conclusiones Referencias GlosarioTabla de las figuras Anexos Anexo 1 - Contenido del plan de estudios de matemáticas, 2010/11 165
Anexo 2 - el centro de las iniciativas promovidas para fomentar la colaboración entre profesores, 2010/11
Anexo 3 - Las tasas de respuesta según el país de la Encuesta de
Formación Inicial de los Profesores de Matemáticas y Ciencias (Sitep) Agradecimientos
domingo, 20 de noviembre de 2011
"Educación científica AHORA. Una pedagogía renovada para el futuro de Europa". El informe Rocard
Una pedagogía renovada para el futuro de Europa
El informe apuesta por reforzar una cultura general más científica. Apuesta por una pedagogía de la ciencia IBSE (Inquiry-Based Science Education) y de las Matemáticas PBL (Problem-based learning). La clave es una actidud innovadora de los profesores y el apoyo institucional en esa línea.
En los últimos tiempos es muy significativo el descenso del interés de los jóvenes europeos (también españoles) por seguir estudios de Matemáticas, Ciencias y Tecnología. Esta situación se considera alarmante porque pone en serio peligro el progreso de la economía europea. Más aún si se compara con la pujanza de los estudios científicos en los países asiáticos.
En la famosa estrategia de Lisboa 2000, que aspiraba a una economía europea basada en el conocimiento, se fijaba como uno de sus objerivos: "Aumentar significativamente el número de titulados en Ciencias y Tecnología y equilibrar el porcentaje de chicos y chicas."
El siguiente gráfico es muy significartivo de la situación que está viviendo Europa.
Situación en España
En España, en los últimos años, también se ha produicido un descenso muy significativo de estudiantes de Ciencias e Ingeniería. En la última década el número de estudiantes en Grados de Ciencias ha disminuido en un 27,3% y en el caso de los estudiantes de ingeniería el descenso ha sido de un 16,4%. Y esto es especialmente grave cuando en ese mismo periodo el número total de estudianntes niversitarios aumentó un 5,6%. Esto es gravísimo para el desarrolllo económico y cultural de un país. Este gráfico tomado del Informe Datos y cifras de la Universidad española 2012-13. (página 11) muestra la evolución en la última década. El pronóstico es claramente ir hacia un empeoramiento de la situación ya que el número de alumnos matriculados en la modalidad de Ciencias del bachillerato está en un progresivo retroceso.
Situación en el mundo de estudios de STEM (Science, Technology and Mathematics)
En Europa, solo el 17% de los alumnos de enseñanzas superiores cursan estas especialidades, mientras que en Corea del Sur optan por ellas el 29% de los estudiantes, y en China y Taiwan el 31%, según datos de la consultora Roland Berger Strategy Consultants. En España solo 13 de cada 1.000 personas han completado estudios en estos campos, según datos de Eurostat.
¿Por qué las chicas no quieren ser ingenieras?
http://www.elmundo.es/espana/2015/07/27/55b025f7268e3e3b6e8b459b.html
El informe Rocard
En este contexto, la Unión Europea encomendó a Michel Rocard, ex primer ministro de Francia, que coordinase el trabajo de una comisión de expertos para estudiar la situación de la enseñanza de las Ciencias. El resultado del trabajo es el informe:
Science Education NOW. A Renewed Pedagogy for the Future of Europe
El contenido tradicido al español:
Educación científica AHORA.Una pedagogía renovada para el futuro de Europa
Experiencias de renovación pedagógica
En el Informe se citan dos ejemplos de programas para la mejora de de la enseñanza de las Ciencias y las Matemáticas. Merece la pena estar al tanto de sus trabajos.
También en ENSEÑAR Y APRENDER MATEMÁTICAS:
jueves, 17 de noviembre de 2011
Proyecto Gauss. Matemáticas 2.0
Después del proyecto Descartes, Desde el Ministerio de Educación se ha impulsado el proyecto Gauss, con el fin de llevar las Nuevas tecnologías a la enseñanza-aprendizaje de la Matemáticas. Merece la pena darse una vuelta y ver lo que hay
sábado, 12 de noviembre de 2011
Para ver las razones trigonométicas. Didáctica analógica y didáctica digital.
Las razones trigonométricas sirven para medir longitudes utilizando ángulos, y ángulos utilizando longitudes.
Para visualizar mecánicamente el significado de las razones trigonométricas y ver, de una manera dinámica, cómo evolucionan al variar la magnuitud del ángulo, se puede utilizar un semicírculo graduado de cartón, un cordel y un poco de alambre.
Winkelfunktionenmesser
Formando parte del histórico Gabinete de matemáticas del Instituto del "Cardenal Cisneros", hemos enconttrado esta pieza de madera forrada de papel en el que se ven escalas graduadas y con textos explicativos en Alemán. Aunque no aparecen fechas, podrían ser de los años cuarenta.
Esta que acabamos de ver, podríamos considerar que es la manera analógica de enseñar el significado de las razones trigonométrica.
El Geogebra, nos ofrece una alternativa digital de estudiar el significado de las funciones trigonométricas. Por ejemplo, se puede ver esta página web.
domingo, 6 de noviembre de 2011
"¡Prohibido NO tocar!" Museos de Matemáticas
“No es lo que importa que el material sea poco o mucho, pobre o rico, grande o pequeño; lo que interesa es que sea adecuado a aquella obra de educación activa, forjadora…y por adecuado, en este respecto, entiendo vivo; y vivo quiere decir, por lo que hace a la escuela primaria, fabricado en ella como obra del trabajo común de maestro y discípulo”
(M. B. Cossío)

Más información sobre Matemathikum de Giessen

[Gracias a mis amigos: Manuel Abellanas, que me habló de Jin Akiyama, y a Kiyoko Kojima, que mellevó hasta estos vídeos en google en japonés]
Video de la inauguración del Museo de Matemáticas de Nueva York
http://www.espace-sciences.org/archives/jsp/fiche_pagelibre_92198600.html
Aprendiendo matematicas (materiales para enseñar matematicas) http://tienda.aprendiendomatematicas.com/
Material didáctico ADRADA.ES http://www.adrada.es/index2/menuprincipal.html
Materiales de fisica http://www.taringa.net/posts/ciencia-educacion/15723920/Mecanica-Eolipila-de-Heron.html
Antiguedades:
http://www.fleaglass.com/
http://www.dorotheum.com
Les fils d'Emile Deyrolle http://www.deyrolle.com/
Geometric Toy
- Materiales para hacer experimentos:
Mates http://why.gr/#/state/itemList/Category/10/SubCategory/10.030/Page/6/language/en_US
Juguetes matemáticos
http://www.grand-illusions.com/acatalog/Maths_Toys.html
Corta y dobla
http://www.cutoutfoldup.com/index.php
¿Por qué les gusta tanto la cicloide a los skaters? La cicloide y sus propiedades. ("Es fácil reconocer al león por sus garras").
La cicloide es la curva que que describe un punto de una circunferncia al rodar sobre una recta.
Es una curva muy fácil de construir por procedimientos mecánicos.
La cicloide es la solución del famoso problema de la braquistrocrona que propuso Johann Bernouilli con idea de poner en ridículo a Newton. [Fuente: Museo de la ciencia ]
Todas las bolas llegan al mismo tiempo, independientemente de su posición inicial en la curva. Esto es la base de un tipo especial de péndulos en los que el periodo no depende de la posioción inicial.
Este vídeo tan simpático nos muestra cómo unos estudiantes americanos se han fabricado una cicloide y explican cómo han experimentado para descubrir sus propiedades.
Es una curva muy fácil de construir por procedimientos mecánicos.
La cicloide es la solución del famoso problema de la braquistrocrona que propuso Johann Bernouilli con idea de poner en ridículo a Newton. [Fuente: Museo de la ciencia ]
Johann Bernoulli, en la Actas de Leipzig, propuso el siguiente problema:la cicloide también es la TAUTOTRONA
Dados dos puntos A y B situados en un plano vertical, entre todas las curvas situadas en el plano vertical, que unen los puntos A y B, determinar la que es recorrida en el menor tiempo posible por un punto móvil M, de masa puntual, sometido a la acción de la gravedad.
Ya Galileo se había hecho la misma pregunta: ¿cuál es el camino que recorre en menor tiempo? No se pide la curva de menor distancia, se quiere calcular la de menor tiempo, la que es recorrida más rápidamente. No haremos los cálculos, pues esto es un Museo de la Ciencia y, como tal, debemos ser divulgativos.
Pero sí diremos la solución: la braquistócrona. Braquistócrona significa, en griego, "tiempo más corto". Aunque el mismo Bernoulli dio una solución en 1697, fue Newton quien la clasificó como una cicloide, es decir, el lugar geométrico descrito por un punto de una circunferencia cuando ésta rueda por una línea recta sin deslizar. El desafortunado Bernoulli lanzó el reto para intentar ridiculizar a Newton, que ya por aquella época se dedicaba a trabajos burocráticos. Bernoulli estaba de parte de Leibniz y pensó que Newton no podría hacer un correcto uso del necesario cálculo diferencial para resolver el problema. Pero sí consiguió resolverlo, y Bernoulli dejó para la historia la frase "Es fácil reconocer al león por sus garras".
Todas las bolas llegan al mismo tiempo, independientemente de su posición inicial en la curva. Esto es la base de un tipo especial de péndulos en los que el periodo no depende de la posioción inicial.
Este vídeo tan simpático nos muestra cómo unos estudiantes americanos se han fabricado una cicloide y explican cómo han experimentado para descubrir sus propiedades.
martes, 1 de noviembre de 2011
El material para la Enseñanza de las Matemáticas que había en el "Cisneros" en el curso 1876-77


Esta réplica del METRO PATRÓN es una muestra del material del antiguo GABINETE DE MATEMÁTICAS del Instituto del Cardenal Cuisneros.
Copiamos el texto del material para la Enseñanza de las Matemáticas que aprece en la memoria del Instittuto del "Cardenal Cisneros" en la memoria del curso 1876-77.
ENSEÑANZA DE MATEMÁTICAS
1. Una colección completa de las pesas y medidas del sistema métrico decimal compuesta de:
Un metro-tipo de acero en su caja,—Otro id. de laton,—Otro id. de madera. Veintisiete medidas de capacidad, unas de latón y otras de madera con aros de hierro.
Ocho pesas de hierro, desde la de 1 hectogramo hasta la de 20 kilogramos.
Un estuche con el kilogramo y sus divisiones hasta el centigramo.
Un pequeño globo terráqueo juntamente con una caja de modelos para explicar el sistema métrico.
2. Una lujosa colección completa de las pesas y medidas de la Villa de Madrid, regalo del Excmo. Ayuntamiento, construida expresamente para este Instituto. Consta de:
Una vara de caoba.
Nueve medidas de estañe para líquidos, desde la arroba a la media copa.
Otras nueve de caoba para áridos, desde la media fanega hasta el ochavillo.
Un precioso estuche con diez pesas de bronce desde la arroba al adarme.
3. Cartabones, reglas y compases de madera para el uso diario de las cátedras de Matemáticas.
4. Veintitrés modelos para el estudio de la Geometría del espacio.
5. Una caja con noventa y tres cuerpos geométricos de madera.
6. Otras varias colecciones construidas por los alumnos del Instituto.
7. Seis piquetes con puntas de hierro.
8. Seis grandes banderolas para el levantamiento de planos.
9. Dos miras de caoba, sistema inglés, de cuatro metros de altura, en su caja.
10. Otra antigua, de haya, de un metro y setenta centímetros.
11. Una cinta de diez metros de longitud.
12. Otra id. de tejido metálico, de cuarenta metros.
13. Una cadena de hierro de diez metros de longitud, con diez agujas,
14. Una escuadra de agrimensor, prisma octogonal de latón.
15. Dos niveles de aire de diez y seis y diez y ocho centímetros,
16. Un nivel de agua en su caja, con trípode correspondiente.
17. Un nivel de aire con anteojo movible en sus collares, caja y trípode.
18.—Otro nivel de aire de Burel, con eclímetro.
19. Otro nivel de aire con pínulas, regalo del actual Sr. Director del Instituto.
20. Otro inglés, superior, de diez y seis pulgadas, con anteojo, del fabricante Casella, que lleva el núm. 352, con su trípode y caja de caoba forrada de cuero.
21. Una plancheta antigua de cincuenta y cuatro centímetros de lado con su trípode y alidada de latón con pínulas, en su caja.
22. Una plancheta de setenta y dos por cincuenta y seis centímetros, con rodillos y trípode del último sistema: la alidada correspondiente lleva anteojo y nivel.
23. Un grafómetro antiguo con brújula y dos niveles con su trípode.
24. Una pequeña brújula con anteojo, en caja de madera de 18 centímetros de lado.
25. Otra nivelante superior con doble graduación, círculo entero, anteojo, plataforma de tres tornillos, señalada con el núm. 7 del fabricante Casella, con trípode y caja forrada de cuero.
26. Escuadra de agrimensor perfeccionada con anteojo, brújula, nivel y círculo graduado; núm. 19 del mismo fabricante, con trípode y caja.
27. Teodolito inglés concéntrico de cinco pulgadas, que aprecia minutos, de la más esmerada construcción del citado fabricante Casella, señalado con el nú-mero 347, con trípode y caja de c i.)ba forrada de cuero.
28. Transportador inglés con circulo ente•ro y graduación sobre plata, que aprecia de veinte en veinte segundos, en su estuche.
29. Un pantógrafo de metal de la mejor construcción en su caja.
30. Un estuche de seis escalas, de marfil, de varias proporciones.
31. Un estuche de matemáticas completo.
32. Paralelas de ébano de treinta y cinco centímetros de longitud.
33. Transportador de talco de forma rectangular.
34. Una pieza de papel de cuarenta y siete centímetros de ancho.—Otra de papel vegetal para calcar, de veinte metros.—Otra de papel cuadriculado.
Suscribirse a:
Entradas (Atom)