
Ya los agrimensores egipcios, hace tres mil años, utilizaban el triángulo de lados 3, 4 y 5 para dibujar ángulos rectos sobre el terreno.
La propiedad de los triángulos rectángulos de afirma que el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos, es el famoso teorema de Pitágoras al que vamos a dedicar este post.
¿Sabrías demostrar el teorema de Pitágoras? ¿Hay más ternas pitagóricas además de (3-4-5) (5-12-13)? ¿Qué tiene esto que ver con el último teorema de Fermat?
Demostración del teorema de Pitágoras de Galileo
Galileo utilizó una balanza para comprobar la igualdad de áreas.Uasando este método, demostró, por ejemplo que el área debajo de una cicloide es igual a la de tres cículos que lo generan.
En el siguiente vídeo vemos cómo el cuadrado construido sobre la hipotenusa pesa lo mismo que los dos cuadrados contruidos sobre los catetos
Vídeo de elaboración propia:
Para ver una amplia explicación de las demostraciones del teorema de Pitágoras usando MOSAICOS PITAGÓRICOS puedes visitar esta entrada del blog
Demostración sin palabras del Teorema de Pitágoras
(Chou pei suan ching 200 a. C.)
Demostración sin palabras del Teorema de Pitágoras
( División de Perigal)
Teorema de Pitágoras - Módulos Interactivos from Principia on Vimeo.
Otra demostración manipulativa del Teorema de Pitágoras (vídeo de elaboración propia)

Demostración acuática:
Demostración de Euclides

Demostración manipulable de Lonardo Da Vinci
Demostración del teorema de Pitágoras del libro "Mirar y ver" de Miguel de Guzmán
Puzzles Pitagóricos
PUZZLES PITAGÓRICOS
Demostración acuática

Puzzle pitagórico
Puzzles pitagórcos para imprimir y hacer on line
Demostración del Teoerema de Pitágoras de A. Einstein
https://pseudopodo.wordpress.com/2008/11/28/pitagoras-segun-einstein/
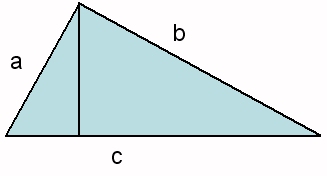
En el triángulo original, de lados a,b,c, trazamos una altura. Se forman así dos nuevos triángulos rectángulos. El de la izquierda tiene por hipotenusa a; llamaremos a su área Sa; el de la derecha tiene por hipotenusa b, y su área será Sb. El triángulo original, con hipotenusa c, tendrá un área Sc.
Estos tres triángulos son semejantes porque tienen ángulos iguales. En el plano euclídeo, el área de cualquier figura geométrica es proporcional al cuadrado de su dimensión lineal. Podemos escribir por tanto que:
Además, es obvio que
Otra demostración manipulativa del Teorema de Pitágoras (vídeo de elaboración propia)

Demostración acuática:
Demostración de Euclides

Demostración manipulable de Lonardo Da Vinci
Demostración del teorema de Pitágoras del libro "Mirar y ver" de Miguel de Guzmán
Puzzles Pitagóricos
PUZZLES PITAGÓRICOS
Demostración acuática

Puzzle pitagórico
Puzzles pitagórcos para imprimir y hacer on line
Demostración del Teoerema de Pitágoras de A. Einstein
https://pseudopodo.wordpress.com/2008/11/28/pitagoras-segun-einstein/
En el triángulo original, de lados a,b,c, trazamos una altura. Se forman así dos nuevos triángulos rectángulos. El de la izquierda tiene por hipotenusa a; llamaremos a su área Sa; el de la derecha tiene por hipotenusa b, y su área será Sb. El triángulo original, con hipotenusa c, tendrá un área Sc.
Estos tres triángulos son semejantes porque tienen ángulos iguales. En el plano euclídeo, el área de cualquier figura geométrica es proporcional al cuadrado de su dimensión lineal. Podemos escribir por tanto que:
Sa = k·a2
Sb = k·b2
Sc = k·c2
donde k es una constante igual en las tres ecuaciones (ya que los
triángulos, al ser semejantes, son la misma figura geométrica).Sb = k·b2
Sc = k·c2
Además, es obvio que
Sc = Sa + Sb
Sustituyendo aquí las ecuaciones anteriores,
c2 = a2 + b2
Demostración del Teorema de Pitágoras como un caso particular del Teorema de Tolomeo
Ternas pitagóricas y el último teorema de Fermat
Además de (3-4-5) hay otras ternas pitagóricas, es decir, tres números enteros (x-y-z) que cumplen el teorema de Pitágoras
x2 + y 2= z2
Por ejemplo: (9-12-15), (5-12-13), ... son ternas pitagóricas

¿Esto mismo funcionará para los cubos?
El último teorema de Fermat, que enunció Fermat sin demostración conocida poco antes de morir, afirma que, si se cambia el exponente 2 por otro entero cualquiera n mayor que 2, la ecuación
Por ejemplo: (9-12-15), (5-12-13), ... son ternas pitagóricas

¿Esto mismo funcionará para los cubos?
x3 + y 3= z3
El último teorema de Fermat, que enunció Fermat sin demostración conocida poco antes de morir, afirma que, si se cambia el exponente 2 por otro entero cualquiera n mayor que 2, la ecuación
xn + y n= zn
no tiene soluciones enteras.
¿Puedes averiguar algo más sobre Fermat? ¿Se ha demostrado ya el último teorema de Fermat?
¿Puedes averiguar algo más sobre Fermat? ¿Se ha demostrado ya el último teorema de Fermat?
En uno de los episodios de los Simpsons se hace referencia al último teorema de Fermat.
Como se puede ver en el fotograma que se ha incluido en el texto aparece la igualdad
178212 + 184112 = 192212
Es curioso, el caso que se presenta, pues si se hace con una calculadora (por cuestiones de redondeo) resulta que se verifica lo que sería un contraejemplo del último teorema de Fermat. ¡Compruébalo!
Para ampliar







10 comentarios:
bn
Gracias por la información! Me ha interesado realizar algunas de estas demostraciones con mis alumnas :)
Interesante información, me ha ayudado a la comprensión del tema
Thanks for your article! I have been looking for quite a long time and fortunately I read this article! I wish you would continue to have valuable articles like this or more to share with everyone!
Demostraciones muy amenas!
Calculadora de Pitágoras
Soy Ángela
No hagan cosas así mandan mucho deber
Si dejen de mandar mucho deber
Confirmo
Nmms ya es 2021
Publicar un comentario